MFP language Help: Mathematic Analysis and Calculation Functions

A big advantage of MFP programming language is its capability of performing mathematical analysis and scientific calculation. This chapter will introduce the related variables and functions.

Section 1  Built-in Constant Variables

In the previous sections user has been demonstrated how to use some of MFP built-in constant variables like i (unit of image value), null, nan and nani. To fully support scientific calculation, MFP also includes the following constant values:

1. Inf, which means real positive infinite. Clearly, -inf means real negative infinite.

2. Infi, which means positive infinite image value. Clearly, -infi means negative infinite image value.

MFP provides this constant variable because infi cannot be obtained from multiplication of inf and i (inf * i == nan + infi), so that a specific variable is required.

3. pi，whose value in MFP  is 3.1415926535897932384626433832795028841971693993751058209749445923.

4. e，whose value in MFP is 2.7182818284590452353602874713526624977572470936999595749669676277.

Section 2  Unit Conversion Functions and Constant Value Functions

MFP programming language provides a unit conversion function, i.e. convert_unit. Convert_unit(value, from_unit, to_unit) converts a value based on from_unit to a new value based on to_unit. Note that both from_unit and to_unit are case sensitive. For example, convert_unit(23.71,"m","km") returns 0.2371.

Convert_unit supports the following units:

1. Length units: "um" (micrometers), "mm" (millimeters), "cm" (centimeters), "m" (meters), "km" (kilometers), "in" (inches), "ft" (feet), "yd" (yards), "mi" (miles), "nmi" (nautical miles), "AU" (astronomical units), "ly" (light years), "pc" (parsec);

2. Area units: "mm2" (square millimeters), "cm2" (square centimeters), "m2" (square meters), "ha" (hectares), "km2" (square kilometers), "sq in" (square inches), "sq ft" (square feet), "sq yd" (square yards), "ac" (acres), "sq mi" (square miles);

3. Volume units: "mL" (milliliters (cc)), "L" (litres), "m3" (cubic meters), "cu in" (cubic inches), "cu ft" (cubic feet), "cu yd" (cubic yards), "km3" (cubic kilometers), "fl oz(Imp)" (fluid ounces (Imp)), "pt(Imp)" (pints (Imp)), "gal(Imp)" (gallons (Imp)), "fl oz(US)" (fluid ounces (US)), "pt(US)" (pints (US)), "gal(US)" (gallon s(US));

4. Mass units: "ug" (micrograms), "mg" (milligrams), "g" (grams), "kg" (kilograms), "t" (tonnes), "oz" (ounces), "lb" (pounds), "jin" (market catties), "jin(HK)" (catties (HK)), "jin(TW)" (catties (TW));

5. Speed units: "m/s" (meters per second), "km/h" (kilometers per hour), "ft/s" (feet per second), "mph" (miles per hour), "knot" (knots);

6. Time units: "ns" (nanoseconds), "us" (microseconds), "ms" (milliseconds), "s" (seconds), "min" (minutes), "h" (hours), "d" (days), "wk" (weeks), "yr" (years);

7. Force units: "N" (newtons), "kgf" (kilogram-forces), "lbF" (pound-forces);

8. Pressure units: "Pa" (pascals), "hPa" (hectopascals), "kPa" (kilopascals), "MPa" (megapascals), "atm" (atomspheres), "psi" (pounds per square inch), "Torr" (torrs (millimeters of mercury);

9. Energy units: "J" (joules), "kJ" (kilojoules), "MJ" (megajoules), "kWh" (kilowatt-hours), "cal" (calories), "kcal" (kilocalories), "BTU" (British Thermal Units);

10. Power units: "W" (Watts), "kW" (kilowatts), "MW" (megawatts), "cal/s" (calories per second), "BTU/h" (BTUs per hour), "hp" (horse powers);

11. Temperature units: "0C" (celsius), "0F" (fahrenheit), "K" (Kelvin);

MFP is also capable of returning some constant values in science. Function get_constant(const_name, n) returns the constant value corresponding to the case-sensitive string const_name. The returned value will be rounded to n significant digits after decimal point. Here n must be non-negative and is optional. If n is neglected, the returned value will not be rounded. This function supports the following constants:

1. Ratio of circumference of a circle to its diameter (const_name == "pi");

2. Natural logarithm (const_name == "e");

3. Light speed in vacuum [m/s] (const_name == "light_speed_in_vacuum");

4. Gravitational constant [m**3/kg/(s**2)] (const_name == "gravitational_constant");

5. Planck constant [J*s] (const_name == "planck_constant");

6. Magnetic constant [N/(A**2)] (const_name == "magnetic_constant");

7. Electric constant [F/m] (const_name == "electric_constant");

8. Elementary charge [c] (const_name == "elementary_charge_constant");

9. Avogadro constant [1/mol] (const_name == "avogadro_constant");

10. Faraday constant [C/mol] (const_name == "faraday_constant");

11. Molar gas constant [J/mol/K] (const_name == "molar_gas_constant");

12. Boltzman constant [J/K] (const_name == "boltzman_constant");

13. Standard gravity [m/(s**2)] (const_name == "standard_gravity");

For example, if user inputs get_constant("pi", 4), the result will be 3.1416; if user inputs get_constant("pi", 8), the result will be 3.14159265; if user inputs get_constant("pi", 0), s\he will get 3; if user inputs get_constant("pi"), the result will be 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 (with 100 digits after decimal point), which is the pi value internally used by the software.

The following example is for the above two functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder.

Help

@language:

  test convert_unit and get_constant functions

@end

@language:simplified_chinese

  测试convert_unit函数和get_constant函数

@end

endh

function getConstCvtUnit()

  print("\nconvert_unit(23.71,\"m3\",\"fl oz(US)\") = " _

    + convert_unit(23.71,"m3","fl oz(US)"))

  print("\nget_constant(\"pi\", 4) = " + get_constant("pi", 4))

  print("\nget_constant(\"pi\", 8) = " + get_constant("pi", 8))

  print("\nget_constant(\"pi\", 0) = " + get_constant("pi", 0))

  print("\nget_constant(\"pi\") = " + get_constant("pi"))

endf

The result of the above example is:

convert_unit(23.71,"m3","fl oz(US)") = 801730.4782606974628681506740932151121554177525643799285007984748218874

get_constant("pi", 4) = 3.1416

get_constant("pi", 8) = 3.14159265

get_constant("pi", 0) = 3

get_constant("pi") = 3.1415926535897932384626433832795028841971693993751058209749445923

Section 3  Trigonometrical Functions and Hyperbolic Functions

Trigonometrical and hyperbolic functions in MFP programming language have the same name and usage as in math. The only thing to keep in mind is, if no d in the end of the function name, calculation result is based on arc, otherwise, it is based on degree. For example, cos(pi/3) returns 0.5, while asind(0.5) is 30, which means 30 degrees. Also note that all these functions support complex calculation, e.g. asind(8) returns 90 – 158.63249757 * i.

All the trigonometrical functions and inverse trigonometrical functions are listed below:

Function name	Function info
acos	acos(1) : acos(x), where x can be a complex number, returns arccos value of x.
acosd	acosd(1) : Function acosd(x) calculates degree based arccos value of x.
asin	asin(1) : asin(x), where x can be a complex number, returns arcsin value of x.
asind	asind(1) : Function asind(x) calculates degree based arcsin value of x.
atan	atan(1) : atan(x) returns arctan value of x, where x can be a complex number.
atand	atand(1) : Function atand(x) calculates degree based arctan value of x.
cos	cos(1) : cos(x) returns cos value of x, where x can be a complex number.
cosd	cosd(1) : Function cosd(x) calculates cos x where x is a degree.
sin	sin(1) : sin(x) returns sin value of x, where x can be a complex number.
sind	sind(1) : Function sind(x) calculates sin x where x is a degree.
tan	tan(1) : tan(x) returns tan value of x, where x can be a complex number.
tand	tand(1) : Function tand(x) calculates tan x where x is a degree.

All the hyperbolic functions are listed below:

Function name	Function info
acosh	acosh(1) : Function acosh(x) calculates inverse hyperbolic cos of x.
asinh	asinh(1) : Function asinh(x) calculates inverse hyperbolic sin of x.
atanh	atanh(1) : Function atanh(x) calculates inverse hyperbolic tan of x.
cosh	cosh(1) : Function cosh(x) calculates hyperbolic cos of x.
sinh	sinh(1) : Function sinh(x) calculates hyperbolic sin of x.
tanh	tanh(1) : Function tanh(x) calculates hyperbolic tan of x.

The following example is for the above two functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder.

Help

@language:

  test trigonometric and hyperbolic trigonometric functions

@end

@language:simplified_chinese

  测试三角函数和双曲三角函数

@end

Endh

function testTrigHTrig()

  print("\ncos(pi/3) = " + cos(pi/3))

  print("\ntand(45) = " + tand(45))

  print("\nsin(1 + 2*i) = " + sin(1 + 2*i))

  print("\nasind(0.5) = " + asind(0.5))

  print("\nacos(8) = " + acos(8))

  print("\nacosh(4.71 + 6.44i) = " + acosh(4.71 + 6.44i))

  print("\nsinh(e) = " + sinh(e))

  print("\natanh(e) = " + atanh(e))

endf

Running the above example user will see:

cos(pi/3) = 0.5

tand(45) = 1

sin(1 + 2*i) = 3.1657785132161682200525265356615738370974142362979081716694416027 + 1.959601041421606115476765045922954107994611047413801140191859959i

asind(0.5) = 30.000000000000003071288025528876242434085090019423660218589920376

acos(8) = -2.768659383313573751905778408399783074855804443359375i

acosh(4.71 + 6.44i) = 2.771116084398325796200879267416894435882568359375 + 0.94305685974139741301058847966487519443035125732421875i

sinh(e) = 7.544137102816974971286612117182812653481960296630859375

atanh(e) = 0.385968416452652396397837719632661901414394378662109375 + 1.5707963267948966192313216916397514420985846996875529104874722962i

. User may notice that, the return value of asind(0.5) is 30.000000000000003071288025528876242434085090019423660218589920376 instead of 30 (degrees). This is because asind first converts the parameter, i.e. 0.5 to a complex value and then does the calculation and calculating asind of a complex value leads to a tiny error.

Section 4  Exponential, Logarithmic and Power Functions

MFP supports a number of exponential, logarithmic and power functions as below:

Function name	Function info
exp	exp(1) : exp(x), where x is a real or complex number, returns x powers of e.
lg	lg(1) : Function lg(x) returns e based log value of x.
ln	ln(1) : Function ln(x) returns e based log value of x.
log	log(1) : log(x), where x can be a complex number, returns e based logarithm value of x.
log10	log10(1) : Function log10(x) returns 10 based log value of x.
log2	log2(1) : Function log2(x) returns 2 based log value of x.
loge	loge(1) : Function loge(x) returns e based log value of x.
pow	pow(2) : pow(x,y) returns y powers of x. Note that both x and y can be either a real or a complex number. If there are more than one results of pow(x,y), return the first result. pow(3) : pow(x,y,z) returns a list including first z values of y powers of x. If y powers of x has less than z values, returns all the values. Note that y must be a real number while x can be either a real or a complex number. Z must be a positive integer.
sqrt	sqrt(1) : Function sqrt(x) returns square root of real number x.

Please note that:

1． Lg(x), log(x), ln(x) and loge(x) all returns natural logarithm of x. Log2(x) returns 2 based logarithm of x. Log10(x) is 10 based. All these functions accept complex value as parameter. Any other base can be obtained from division of these functions. For example, user simply uses log(x)/log(3) to get 3 based logarithm of x.

2． There are two ways to call pow function. First is pow(x, y), which returns x^y. Note that both x and y can be either real or complex value. If the result have many values, this function returns the first value it sees when anti-clockwisely rotating from 0 degree in the complex domain. This usage equals using x**y. For example, pow(32, 0.2) returns 2. However, pow(-32, 0.2) will not returns -2 although -2 is one of its roots. Instead, it returns 1.61803399 + 1.1755705 * i.

The second way to call pow function is pow(x, y, z), which returns the first z results of x^y. Here y must be a real value while x can be either real or complex. Z should be a positive integer. The returned values are stored in a vector. If the number of results is less than z, all the results are returned. Otherwise, it returns the first z results it sees when anti-clockwisely rotating from 0 degree in the complex domain. For example, if user wants to see all the results of -32^0.2, pow(-32, 0.2, 5) can be called and a 5-element vector, i.e. [1.61803399 + 1.1755705 * i, -0.61803399 + 1.90211303 * i, -2, -0.61803399 - 1.90211303 * i, 1.61803399 - 1.1755705 * i], is returned.

3． Sqrt(x) is equal to x**0.5 or pow(x, 0.5). It returns the first square root seen when rotating anti-clockwisely from 0 degree in the complex domain. For example, sqrt(4) == 2, sqrt(-2) == 1.41421356 * i and sqrt(-2+3i) == 0.89597748 + 1.67414923 * i.

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder.

Help

@language:

  test log, exp and pow and related functions

@end

@language:simplified_chinese

  测试对数，指数和次方函数

@end

endh

function testLogExpPow()

  print("\nlg(e) == " + lg(e))

  print("\nlog(9, 3) == log(9)/log(3) == " + log(9)/log(3))

  print("\nlog2(3 + 4i) == " + log2(3 + 4i))

  print("\npow(32, 0.2) == " + pow(32, 0.2))

  print("\npow(-32, 0.2) == " + pow(-32, 0.2))

  print("\npow(-32, 0.2, 5) == " + pow(-32, 0.2, 5))

  print("\nsqrt(4) == " + sqrt(4))

  print("\nsqrt(-2) == " + sqrt(-2))

  print("\nsqrt(-2+3i) == " + sqrt(-2+3i))

endf

The result of the above example is shown below:

lg(e) == 1

log(9, 3) == log(9)/log(3) == 2

log2(3 + 4i) == 2.3219280948873622916712631553180615794157506196217129274315603707 + 1.337804212450976175615004492526409565791145361743891813677556325i

pow(32, 0.2) == 2

pow(-32, 0.2) == 1.6180339887498949025257388711906969547271728515625 + 1.175570504584946274206913585658185184001922607421875i

pow(-32, 0.2, 5) == [1.6180339887498949025257388711906969547271728515625 + 1.175570504584946274206913585658185184001922607421875i, -0.6180339887498946804811339461593888700008392333984375 + 1.90211303259030728440848179161548614501953125i, -2, -0.6180339887498951245703437962220050394535064697265625 - 1.9021130325903070623638768665841780602931976318359375i, 1.6180339887498946804811339461593888700008392333984375 - 1.17557050458494671829612343572080135345458984375i]

sqrt(4) == 2

sqrt(-2) == 1.4142135623730951454746218587388284504413604736328125i

sqrt(-2+3i) == 0.8959774761298379706375607865525069497958199765590683867889064147 + 1.6741492280355400682758136732173307274213575287387175311747860088i

Section 5  Matrix Related Functions

Chapter 4 demonstrates user how to use functions to operate MFP arrays. In this section, more functions for matrix calculation are introduced.

In MFP, array is different from matrix. MFP matrix is a mathematical concept. It must be an array. It also supports many mathematical calculations, e.g. +, -, *, /, etc. Moreover, it has to be two dimensional, and in many cases it is a square matrix. The functions for matrix calculation generally cannot be used for common MFP arrays.

MFP matrix calculation functions are listed below:

Function name	Function info
adj	adj(1) : adj(x), where x is 2D square matrix, returns the adjugate matrix of x.
cofactor	cofactor(1) : cofactor(x), where x is 2D square matrix, returns the cofactor matrix of x.
det	det(1) : Function det(x) calculates determinant of square matrix x.
deter	deter(1) : Function deter(x) calculates determinant of square matrix x.
dprod	dprod(2) : Function dprod calculates dot product of two vectors [x1, x2, ... xn] and [y1, y2, ... yn].
eig	eig(1) : eig(A) calculates 2D square matrix A's eigen vectors and eigen values. This function returns a two element list. First element is the eigen vector matrix, each column is an eigen vector. Second element is a diagonal matrix. Each diagonal element is an eigen value. Note that this function needs big memory to run and consumes significant CPU time. If it runs in mobile device, size of A and B should be no greater than 6*6. If it runs in PC, A and B should be no greater than 8*8. Otherwise, it may fail because lack of memory or run for very long time. eig(2) : eig(A, B) calculates 2D square matrix A's eigen vectors and eigen values against same size matrix B, i.e. Av = lambda * Bv, where lambda is an eigen value and v is an eigen vector. The second parameter, B, is optional. By default, B is an I matrix. This function returns a two element list. First element is the eigen vector matrix, each column is an eigen vector. Second element is a diagonal matrix. Each diagonal element is an eigen value. Note that this function needs big memory to run and consumes significant CPU time. If it runs in mobile device, size of A and B should be no greater than 6*6. If it runs in PC, A and B should be no greater than 8*8. Otherwise, it may fail because lack of memory or run for very long time.
get_eigen_values	get_eigen_values(1) : get_eigen_values(A) calculates 2D square matrix A's eigen values. This function returns an eigen value list which includes all the eigen values including duplicated ones. Note that this function needs big memory to run and consumes significant CPU time. If it runs in mobile device, size of A and B should be no greater than 6*6. If it runs in PC, A and B should be no greater than 8*8. Otherwise, it may fail because lack of memory or run for very long time. get_eigen_values(2) : get_eigen_values(A, B) calculates 2D square matrix A's eigen values against same size matrix B, i.e. Av = lambda * Bv, where lambda is an eigen value and v is an eigen vector. The second parameter, B, is optional. By default, B is an I matrix. This function returns an eigen value list which includes all the eigen values including duplicated ones. Note that this function needs big memory to run and consumes significant CPU time. If it runs in mobile device, size of A and B should be no greater than 6*6. If it runs in PC, A and B should be no greater than 8*8. Otherwise, it may fail because lack of memory or run for very long time.
invert	invert(1) : invert(x) inverts 2D matrix x. Note that the elements of x can be complex numbers but x must be a square matrix (i.e. number of rows equals number of columns).
left_recip	left_recip(1) : left_recip(x) calculates left-division reciprocal of x. Note that so far x can only be a number or a 2D matrix.
rank	rank(1) : rank(matrix) returns the rank of a matrix. For example rank([[1,2],[2,4]]) returns 1.
recip	recip(1) : recip(x) calculates reciprocal of x. Note that so far x can only be a number or a 2D matrix.

User may note that:

1. Functions recip, left_recip and invert are actually the same thing for a 2-D square matrix x, which are equal to calculating 1/x.

2. Det and deter are two names for the same function. Their usage and calculation are exactly the same.

3. All the above functions support complex matrix.

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder:

Help

@language:

test matrix functions

@end

@language:simplified_chinese

测试矩阵相关函数

@end

endh

function testMatrix()

print("\ncofactor([[1,3,-4.81-0.66i],[-0.91i,5.774,3.81+2.03i],[0,-6,-7.66-3i]])=" _

+ cofactor([[1,3,-4.81-0.66i],[-0.91i, 5.774, 3.81+2.03i],[0, -6, -7.66-3i]]))

print("\nadj([[1,-7],[-4, 6]]) = " + adj([[1,-7],[-4, 6]]))

print("\ndet([[2.7-0.4i, 5.11i],[-1.49, -3.87+4.41i]]) = " _

+ det([[2.7-0.4i, 5.11i],[-1.49, -3.87+4.41i]]))

print("\ndprod([1,2,3],[4,5,6]) = " + dprod([1,2,3],[4,5,6]))

print("\neig([[1,0],[0,1]]) = " + eig([[1,0],[0,1]]) )

print("\neig([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]])=" _

+ eig([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]]))

print("\nget_eigen_values([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]])=" _

+get_eigen_values([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]]))

print("\nrank([[1,2,3],[4,5,8]]) = " _

+ rank([[1,2,3],[4,5,8]]))

Endf

The result of the above example is:

cofactor([[1,3,-4.81-0.66i],[-0.91i,5.774,3.81+2.03i],[0,-6,-7.66-3i]])=[[-21.3688399999999999999999999999999999999999999999999999999999999986 - 5.1419999999999999999999999999999999999999999999999999999999999994i, 2.73 - 6.9706i, 5.46i], [51.84 + 12.96i, -7.66 - 3i, 6], [39.2029399999999999999999999999999999999999999999999999999999999999 + 9.9008400000000000000000000000000000000000000000000000000000000001i, -4.4106 + 2.3471i, 5.774 + 2.73i]]

adj([[1,-7],[-4, 6]]) = [[6, 7], [4, 1]]

det([[2.7-0.4i, 5.11i],[-1.49, -3.87+4.41i]]) = -8.685 + 21.0689i

dprod([1,2,3],[4,5,6]) = 32

eig([[1,0],[0,1]]) = [[[0, 0], [0, 0]], [[1, 0], [0, 1]]]

eig([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]])=[[[0.5823305472444549220819340004695808799844908575313355771049880239 + 2.6809072575482156074378495725434812981406213152515868875585567468i, 0.0114135820466395502054852954488256551817471139007810529210119208 + 3.4394330048873032459793824252367034270060295989773214887206842872i, 0.1388649308606510232042228769561980233759262865380815606646575143 - 0.6869355577206501991055143100875158982393429000524385229074545558i], [0.1706650271410734493686782716838420204556348720948784459123114335 + 3.2610379517684265529500566832795301074088302158506118107692861942i, 1.0352846399044520080844175395063017457192992181908246617872107954 + 2.0718315370680215726468326567580658394348957576054643511780204727i, 1], [1, 1, -1.4604755542403403454627560718567442382313962988887573353544007743 + 0.5989937399782723545797394498168180189451427644426167079112280372i]], [[1.6771119760640303234132562527571544811705507223533275701869437736 - 1.6789870982611406187191411771858177830523877216751181685694659201i, 0, 0], [0, 0.0328711162943186887885582860890803241425541594114635568073761979 + 0.5055670540754347904151221100125363969735197371948964385418564962i, 0], [0, 0, -0.7099830923583490122018145388462348053131048817647911269943199715 - 8.3365799558142941716959809328267186139211320155197782699723905761i]]]

get_eigen_values([[1+3.7i,-0.41-2.93i,5.33+0.52i],[0.33+2.71i,-3.81i,0.41+3.37i],[2.88,0,-9.4i]])=[1.6771119760640303234132562527571544811705507223533275701869437736 - 1.6789870982611406187191411771858177830523877216751181685694659201i, 0.0328711162943186887885582860890803241425541594114635568073761979 + 0.5055670540754347904151221100125363969735197371948964385418564962i, -0.7099830923583490122018145388462348053131048817647911269943199715 - 8.3365799558142941716959809328267186139211320155197782699723905761i]

rank([[1,2,3],[4,5,8]]) = 2

Section 6  Functions for Expression Calculation and Calculus

Functions for expression calculation and calculus accept string based MFP expression(s) and carry out corresponding calculations. They are:

Function name	Function info
deri_ridders	deri_ridders(4) : deri_ridders(expr, var, val, ord) calculates ord-order derivative value of expression expr which is based on variable var when the variable's value is equal to val. This function always uses Ridders method. For example, deri_ridders("x**2+x","x",3,2) returns 2.
derivative	derivative(2) : derivative(expression, variable) calculates derivative of expression which is based on variable. Note that both expression and variable must be strings. For example, derivative("x**2+x","x") returns a string based expression which is "2*x+1". derivative(4) : derivative(expr, var, val, method) calculates derivative value of expression expr which is based on variable var when the variable's value is equal to val. The parameter method selects the method to use. True means using Ridders method while false means simply calculating derivative expression value at val. For example, derivative("x**2+x","x",2,true) returns 5.
evaluate	evaluate(1...) : evaluate(expr_string,var_string1,var_value1,var_string2,var_value2, ...) returns the value of string based expression expr_string when the string based variable var_string1 equals var_value1, variable var_string2 equals var_value2, ... respectively. Note that var_value1, var_value2, ... can be any type and the number of variables can be zero, i.e. evaluate("3+2") is valid.
integrate	integrate(2) : integrate(x,y) returns the indefinite integrated expression of expression x with respect to variable y where x and y are both strings. Note that if x cannot be indefinitely integrated or x is too complicated to solve, this function throws an exception. integrate(4) : integrate(x,y,z,w) returns the integrated value of expression x with respect to variable y changing from z to w. Note that x and y are string typed and z and w can be real numbers, complex numbers or strings. The integrating algorithm selected is adaptive Gauss-Kronrod method. integrate(5) : integrate(x,y,z,w,v) returns integrated value given a string expression x of a variable y (also a string) and an interval [z, w]. In calculation, one step length is (w - z)/v, note that v must be a positive integer while w and z can be real numbers, complex values or strings. If v is zero, this function is the same as integrate(x,y,z,w).
lim	lim(3) : lim(expr, var, dest_value) calculates the limit value of expression expr when variable var is closing to dest_value. expr and var should be strings and dest_value can be expression or value, whether string based or not. For example, lim("1/x", "x", 0) or lim("(x+2)/(x+3)","x","3+0"). Note that this function is still under development.
product_over	product_over(3) : product_over(x, y, z) calculates the product of string based expression x over integer value y to z. Note that y and z are also string based values, y should be written like "a=10" (where a is the variable) and z should be like "20". For example, product_over("x+1", "x=1", "10").
sum_over	sum_over(3) : sum_over(x, y, z) calculates the sum of string based expression x over integer value y to z. Note that y and z are also string based values, y should be written like "a=10" (where a is the variable) and z should be like "20". For example, sum_over("x+1", "x=1", "10").

Function deri_ridders calculates first, second or third derivative value of a given expression at a given point using Ridders method. The example, deri_ridders("x**2+x", "x", 3, 2), means calculating second derivative value of x**2+x when x equals 3.

Derivative calculates first derivative value of a given expression at a given point, or first derivative expression of a given expression. The first example, derivative("x**2+x","x"), means calculating first derivative expression of x**2+x. The second example, derivative("x**2+x","x", 2, true), means calculating first derivative value of x**2+x when x is 2. Note that the last parameter tells the function whether to use Ridders method or not. If it is true, Ridders method is used. If false, this function first calculates derivative expression, and then gives out the derivative value from the derivative expression. The last parameter is optional. By default, it is true.

Derivative function can also calculate higher order derivative expression. This needs nested calls. For example, derivative(derivative("x**2+x","x"),"x") gives out second derivative expression of x**2+x.

Function sum_over is the sum operator ∑ in math, and its usage is the same as ∑. For example, sum_over("x+1", "x=1", "10") means calculating sum of x + 1s where x is an integer varying from 1 to 10. Using a mathematical expression it is ∑x=110(x+1).

Similar to sum_over, product_over means ∏ in math, and its usage is the same as ∏. For example, product_over("x+1", "x=1", "10") means calculating product of all x + 1s where x is an integer varying from 1 to 10. Using a mathematical expression it is ∏x=110(x+1).

Function evaluate evaluates a string based MFP expression. If this expression has one or more variables, evaluate function takes additional parameters to assign values to the variables so that it is able to give out the calculated result. For example, evaluate("x+y+1","x",3,"y",4) calculates the value of x + y + 1 where x is 3 and y is 4. Clearly, the final result is 8. Of course, if no variable is used in the expression, no additional parameters are required.

Function evaluate can also evaluate functions, whether the to-be-evaluated function is user-defined or system provided. For example, evaluate("sind(30)") returns 0.5.

Function integrate calculates definite or indefinite integrals. In fact, the integration tool in Scientific Calculator Plus is based on this function. It is quite simple to calculate indefinite integrals. Only two parameters are needed. The first one is the expression to be integrated. The second one is variable name. Both of them are based on string. For example,

integrate("cos(x)","x")

calculates integration of cos(x), and the returned result is also a string which is "sin(x)".

There are two numerical methods to calculate definite integrals. First is using Gauss-Kronrod method. This method is able to handle the case where from and/or to value(s) are infinite. It is also able to process high-frequently oscillating functions. It is even capable of integrating functions with singular points. For example,

integrate("exp(x)","x",-inf,0)

returns the integrated value of exp(x) where x is from negative infinite to 0, and the result is 1. For another example,

integrate("log(x)","x",0,1)

calculates the integrated value of log(x) where x is from 0 to 1. The returned result is 1.00000018 (which includes a small error). Note that here 0 is a singular point.

Although Gauss-Kronrod method is powerful, it is very slow. Most of the functions, however, can adopt the traditional Riemann Sum integration algorithm which is much faster with reasonable accuracy. User, as such, needs to indicate the number of steps. Nevertheless, if the number of steps is zero, or from and/or to value(s) are infinite, integrate function still uses Gauss-Kronrod method. An example using Riemann Sum integration algorithm is:

integrate("x**2+1","x", -3+4i, 7-9i, 100)

. This example integrates x**2 + 1 in the complex domain. The number of steps is 100. The final result is -481.7345 - 225.69505 * i. Theoretical result is -481.66666667 - 225.66666667 * i which means the error will be very small if the number of steps is big enough.

User can also calculate higher-order integrals using nested integrate functions. For example,

integrate("integrate(\"x*y\",\"x\",1,6,100)","y",-4,3,100)

integrates x*y where x is from 1 to 6 and y is from -4 to 3. The result is -61.25.

Because in general higher-order integrals need much more calculation steps than first-order integral, Riemann Sum method is strongly recommended as it is fast. This is why the number of steps is not optional in higher-order integration.

Nevertheless, some integrals cannot be calculated by integrate function, e.g. very complicated integrals or integrals which cannot converge. In this case, an exception will be thrown. For example, running the following statements (by copying them and pasting them into GUI based Scientific Calculator Plus for JAVA, and then pressing ENTER key):

try

print("integrate(\"e**(x**2)\",\"x\")", integrate("e**(x**2)","x"))

catch

print("e**(x**2) cannot be integrated")

endtry

, user will see an exception printed:

e**(x**2) cannot be integrated

, which means  is not capable of being integrated.

Also note that the functions introduced in this section are able to read values of declared variables. For instance, assume that in a program a variable b has been declared and its value is 3. If user calls evaluate("x+b","x",9), 12 will be returned. Because of this feature, it is recommended to use different variable name(s) in the maths expression parameter(s) to avoid potential conflict(s). This requirement is particularly important when calculating higher-order integrals.

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder:

Help

@language:

  test expression and calculus functions

@end

@language:simplified_chinese

  测试表达式和微积分相关函数

@end

endh

function exprcalculus()

  print("\nderivative(\"1/x**2*log(x) + 9\", \"x\") = " _

    + derivative("1/x**2*log(x) + 9", "x"))

  print("\nderivative(\"tanh(x)**-1\", \"x\") = " _

    + derivative("tanh(x)**-1", "x"))

  // test high order derivative

  print("\nderivative(derivative(\"x*sin(x)\", \"x\"), \"x\") = " _

    + derivative(derivative("x*sin(x)", "x"), "x"))

  // test derivative value

  print("\nderi_ridders(\"x**0.5+x+9\", \"x\", 0.3, 1) = " _

    + deri_ridders("x**0.5+x+9", "x", 0.3, 1))

  print("\nderivative(\"x**0.5+x+9\", \"x\", 0.3) = " _

    + derivative("x**0.5+x+9", "x", 0.3))

  print("\nderi_ridders(\"x**0.5+sqrt(sin(x**2))\", \"x\", 0.3, 3) = " _

    + deri_ridders("x**0.5+sqrt(sin(x**2))", "x", 0.3, 3))

  print("\nsum_over(\"1/(x-10)\",\"x=1\",\"9\") = " _

    + sum_over("1/(x - 10)", "x = 1", "9"))

  print("\nproduct_over(\"1/(x-10)\",\"x=9\",\"1\") = " _

    + product_over("1/(x-10)", "x = 9", "1"))

  print("\nevaluate(\"x+y+1\",\"x\",5,\"y\",7) = " _

    + evaluate("x+y+1","x",5,"y",7))

  print("\nevaluate(\"sind(30)\") = " + evaluate("sind(30)"))

  print("\nintegrate(\"tanh(x)**-1\",\"x\") = ")

  print(integrate("tanh(x)**-1","x"))

  print("\nintegrate(\"sinh(x)*cosh(x)**-1\",\"x\") = ")

  print(integrate("sinh(x)*cosh(x)**-1","x"))

  print("\nintegrate(\"1/x**2\",\"x\",2,inf) = ")

  print(integrate("1/x**2","x",2,inf))

  print("\nintegrate(\"1/x**2\",\"x\",2,50,100) = ")

  print(integrate("1/x**2","x",2,50,100))

  // test unintegratable.

  try

  print("integrate(\"e**(x**2)\",\"x\")", integrate("e**(x**2)","x"))

  catch

  print("e**(x**2) cannot be integrated")

  endtry

  // test high order integration

  print("\nintegrate(\"integrate(\\\"x*y\\\",\\\"x\\\",1,6,100)\",\"y\",-4,3,100) = ")

  print(integrate("integrate(\"x*y\",\"x\",1,6,100)","y",-4,3,100))

endf

Output of the above example is:

derivative("1/x**2*log(x) + 9", "x") = (-2)*log(x)*x**(-3)+x**(-3)

derivative("tanh(x)**-1", "x") = -(-0.5)*2.7182818284590452353602874713526624977572470936999595749669676277**x*(sinh(x)/cosh(x))**(-2)*sinh(x)*cosh(x)**(-2)+(-0.5)*2.7182818284590452353602874713526624977572470936999595749669676277**(-x)*(sinh(x)/cosh(x))**(-2)*sinh(x)*cosh(x)**(-2)+(-0.5)*2.7182818284590452353602874713526624977572470936999595749669676277**x*(sinh(x)/cosh(x))**(-2)/cosh(x)+(-0.5)*2.7182818284590452353602874713526624977572470936999595749669676277**(-x)*(sinh(x)/cosh(x))**(-2)/cosh(x)

derivative(derivative("x*sin(x)", "x"), "x") = (-1)*x*sin(x)+2*cos(x)

deri_ridders("x**0.5+x+9", "x", 0.3, 1) = 1.9128709291772078606011099231055019184972226816921057762830380748

derivative("x**0.5+x+9", "x", 0.3) = 1.91287092917527690172363463716465048491954803466796875

deri_ridders("x**0.5+sqrt(sin(x**2))", "x", 0.3, 3) = 7.1575232288636571107632429280365926329437264758531027037489228909

sum_over("1/(x-10)","x=1","9") = -2.828968253968253968253968253968253968253968253968253968253968254

product_over("1/(x-10)","x=9","1") = -0.0000027557319223985890652557319223985890652557319223985890652557

evaluate("x+y+1","x",5,"y",7) = 13

evaluate("sind(30)") = 0.5

integrate("tanh(x)**-1","x") = log(sinh(x))

integrate("sinh(x)*cosh(x)**-1","x") = log(cosh(x))

integrate("1/x**2","x",2,inf) = 0.4999999999999999800759152415811779636542182411236778807349767932

integrate("1/x**2","x",2,50,100) = 0.4847465087006575124658317917505673256758819785394978030710821748e**(x**2) cannot be integrated

integrate("integrate(\"x*y\",\"x\",1,6,100)","y",-4,3,100) = -61.25

. Note that in version 1.7, citingspace was introduced into MFP programming language. As such, when calculating indefinite integrals or derivative expressions in this version, each function the answer includes complete citingspace path. For example, log(x) in older versions turns to ::mfp::math::log_exp::log(x) in version 1.7. This change makes the answer longer and hard to read. So from version 1.7.1 it is improved to only show the minimum citingspace path in the result. In other words, ::mfp::math::log_exp::log(x) is returned back to log(x) gain.

Section 7  Statistic, Stochastic and Sorting Functions

Scientific Calculator Plus provides a number of statistic, stochastic and sorting functions as below:

Function name	Function info
avg	avg(1...) : Function avg(...) returns average value of an arbitrary number of parameters.
beta	beta(2) : Function beta(z1, z2) returns beta function value of complexes z1 and z2, note that real part of z1 and z2 must be positive.
gamma	gamma(1) : Function gamma(z) returns gamma function value of complex z, note that real part of z must be positive.
gavg	gavg(1...) : Function gavg(...) returns geometric mean value of an arbitrary number of parameters.
havg	havg(1...) : Function havg(...) returns harmonic mean value of an arbitrary number of parameters.
max	max(1...) : Function max(...) returns maximum value of an arbitrary number of parameters.
med	med(1...) : Function med(...) returns medium value of an arbitrary number of parameters. If the number of parameters is even, returns average of the middle two parameters.
min	min(1...) : Function min(...) returns minimum value of an arbitrary number of parameters.
quick_sort	quick_sort(2) : Function quick_sort(desc, original_list) returns a sorted list of an arbitrary number of parameters. If desc is true (or 1), list elements are from largest to smallest, otherwise (desc is false or 0), from smallest to largest. For example, quick_sort(1, [5,6,7,9,4])'s result is [9,7,6,5,4] while quick_sort(0, [5,6,7,9,4]) is [4,5,6,7,9].
ncr	ncr(2) : Function nCr(x, y) calculates the number of y-combination of a set S which has x elements. Note that x, y are non-negative integers, x >= y.
npr	npr(2) : Function nPr(x, y) calculates the number of y-permutation of a set S which has x elements. Note that x, y are non-negative integers, x >= y.
rand	rand(0) : rand() function returns a random float number between 0 (inclusive) and 1 (exclusive).
stdev	stdev(1...) : Function stdev(...) returns standard deviation of an arbitrary number of parameters. Note that the parameters are a sample of a larger set.
stdevp	stdevp(1...) : Function stdevp(...) returns standard deviation of an arbitrary number of parameters.
sum	sum(1...) : Function sum(...) returns sum value of an arbitrary number of parameters.

Note that functions stdev and stdevp are different. If the two functions have same parameters which are x₁，x₂，x₃，…，x_N , stdev returns

 

, while stdevp returns

 

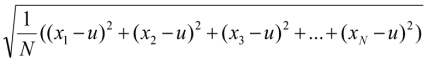
. u here is the average value of x₁，x₂，x₃，…，x_N .

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder:

Help

@language:

  test statistics and sorting functions

@end

@language:simplified_chinese

  测试统计、随机和排序相关函数

@end

endh

function testStatSort()

  print("\navg(1,5,9,-6,3,-18,7) = " + avg(1,5,9,-6,3,-18,7))

  print("\nbeta(3.71, 23.55) = " + beta(3.71, 23.55))

  print("\ngamma(5.44 - 10.31i) = " + gamma(5.44 - 10.31i))

  print("\ngavg(1,5,9,-6,3,-18,7) = " + gavg(1,5,9,-6,3,-18,7))

  print("\nhavg(1,5,9,-6,3,-18,7) = " + havg(1,5,9,-6,3,-18,7))

  print("\nmax(1,5,9,-6,3,-18,7) = " + max(1,5,9,-6,3,-18,7))

  print("\nmed(1,5,9,-6,3,-18,7) = " + med(1,5,9,-6,3,-18,7))

  print("\nmin(1,5,9,-6,3,-18,7) = " + min(1,5,9,-6,3,-18,7))

  print("\nquick_sort(1,[1,5,9,-6,3,-18,7]) = " _

    + quick_sort(1,[1,5,9,-6,3,-18,7]))

  print("\nquick_sort(0,[1,5,9,-6,3,-18,7]) = " _

    + quick_sort(0,[1,5,9,-6,3,-18,7]))

  print("\nstdev(1,5,9,-6,3,-18,7) = " + stdev(1,5,9,-6,3,-18,7))

  print("\nstdevp(1,5,9,-6,3,-18,7) = " + stdevp(1,5,9,-6,3,-18,7))

  print("\nsum(1,5,9,-6,3,-18,7) = " + sum(1,5,9,-6,3,-18,7))

  print("\nncr(8,3) = " + ncr(8,3))

  print("\nnpr(8,3) = " + npr(8,3))

  print("\nrand() = " + rand())

endf

The above example outputs the follows:

avg(1,5,9,-6,3,-18,7) = 0.1428571428571428571428571428571428571428571428571428571428571429

beta(3.71, 23.55) = 0.0000279537392314725872716390423881975646941670888511331711318296

gamma(5.44 - 10.31i) = 0.0015360621732035695620552936894943183717820318136617456390043119 - 0.0279816213196075726360710743099268272949427989554500480691282345i

gavg(1,5,9,-6,3,-18,7) = 5.194584255413065676521000568754971027374267578125

havg(1,5,9,-6,3,-18,7) = 4.472616632860040567951318458417849898580121703853955375253549696

max(1,5,9,-6,3,-18,7) = 9

med(1,5,9,-6,3,-18,7) = 3

min(1,5,9,-6,3,-18,7) = -18

quick_sort(1,[1,5,9,-6,3,-18,7]) = [9, 7, 5, 3, 1, -6, -18]

quick_sort(0,[1,5,9,-6,3,-18,7]) = [-18, -6, 1, 3, 5, 7, 9]

stdev(1,5,9,-6,3,-18,7) = 9.3528707077661721314143505878746509552001953125

stdevp(1,5,9,-6,3,-18,7) = 8.65907569182385117301237187348306179046630859375

sum(1,5,9,-6,3,-18,7) = 1

ncr(8,3) = 56

npr(8,3) = 336

rand() = 0.67638281271680666950629756684065796434879302978515625

Section 8  Signal Processing Functions

Signal processing functions are included in Scientific Calculator Plus for electrical engineers. There are three functions, conv (convolution), FFT (Fast Fourier Transform), iFF (Inverse Fast Fourier Transform):

Function name	Function info
conv	conv(2) : conv(input_a, inputb) returns convolution of input_a and input_b. input_a and input_b can either be two 1-D lists or two 2-D arrays. So far conv function only support 1-D and 2-D convolution. For example, conv([4,8,2,9],[5,3,8,9,6,7,8]) = [20, 52, 66, 151, 139, 166, 181, 132, 79, 72] conv([[4,8,2,9],[8,6,7,9],[2,2,8,-4]],[[-5,i,7],[0.6,8,4]]) = [[-20, -40 + 4 * i, 18 + 8 * i, 11 + 2 * i, 14 + 9 * i, 63], [-37.6, 6.8 + 8 * i, 102.2 + 6 * i, 50.4 + 7 * i, 129 + 9 * i, 99], [-5.2, 57.6 + 2 * i, 58.2 + 2 * i, 119.4 + 8 * i, 156 - 4 * i, 8], [1.2, 17.2, 28.8, 69.6, 0, -16]]
FFT	FFT(1...) : Function FFT(a, ...) returns Fast Fourier Transform of a series of values, note that the number of values in the series should always be 2 to a positive integer. If a is a list of real or complex numbers, this function should only have one parameter and return Fast Fourier Transform of a[0], a[1], ... a[N-1] where N is the number of elements in a. If a is a single value (real or complex), this function should have at least two parameters and return Fast Fourier Transform of a, optional_params[0], optional_params[1], ..., optional_params[number_of_optional_params - 1]. The returned value is always an array. Examples of this function: FFT(1, 2, 3, 4) returns [10, -2 + 2i, -2, -2 - 2i]; FFT([1, 2, 3, 4]) also returns [10, -2 + 2i, -2, -2 - 2i].
IFFT	IFFT(1...) : Function IFFT(a, ...) returns Inverse Fast Fourier Transform of a series of values, note that the number of values in the series should always be 2 to a positive integer. If a is a list of real or complex numbers, this function should only have one parameter and return Inverse Fast Fourier Transform of a[0], a[1], ... a[N-1] where N is the number of elements in a. If a is a single value (real or complex), this function should have at least two parameters and return Inverse Fast Fourier Transform of a, optional_params[0], optional_params[1], ..., optional_params[number_of_optional_params - 1]. The returned value is always an array. Examples of this function: IFFT(10, -2 + 2i, -2, -2 - 2i) returns [1, 2, 3, 4]; IFFT([10, -2 + 2i, -2, -2 - 2i]) returns [1, 2, 3, 4];

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder:

Help

@language:

  test sign processing functions

@end

@language:simplified_chinese

  测试信号处理相关函数

@end

endh

function testSignalProc()

  print("\nconv([4,8,2,9],[5,3,8,9,6,7,8]) = " _

    + conv([4,8,2,9],[5,3,8,9,6,7,8]))

  print("\nconv([[4,8,2,9],[8,6,7,9],[2,2,8,-4]],[[-5,i,7],[0.6,8,4]]) = " _

    + conv([[4,8,2,9],[8,6,7,9],[2,2,8,-4]],[[-5,i,7],[0.6,8,4]]))

  print("\nFFT(1, 2, 3, 4) = " + FFT(1, 2, 3, 4))

  print("\nFFT([1,2,3,4]) = " + FFT([1,2,3,4]))

  print("\niFFT(10, -2 + 2i, -2, -2 - 2i) = " _

    + IFFT(10, -2 + 2i, -2, -2 - 2i))

  print("\niFFT([10, -2 + 2i, -2, -2 - 2i]) = " _

    + IFFT([10, -2 + 2i, -2, -2 - 2i]))

Endf

The above example gives the following results:

conv([4,8,2,9],[5,3,8,9,6,7,8]) = [20, 52, 66, 151, 139, 166, 181, 132, 79, 72]

conv([[4,8,2,9],[8,6,7,9],[2,2,8,-4]],[[-5,i,7],[0.6,8,4]]) = [[-20, -40 + 4i, 18 + 8i, 11 + 2i, 14 + 9i, 63], [-37.6, 6.8 + 8i, 102.2 + 6i, 50.4 + 7i, 129 + 9i, 99], [-5.2, 57.6 + 2i, 58.2 + 2i, 119.4 + 8i, 156 - 4i, 8], [1.2, 17.2, 28.8, 69.6, 0, -16]]

FFT(1, 2, 3, 4) = [10, -2 + 2i, -2, -2 - 2i]

FFT([1,2,3,4]) = [10, -2 + 2i, -2, -2 - 2i]

iFFT(10, -2 + 2i, -2, -2 - 2i) = [1, 2, 3, 4]

iFFT([10, -2 + 2i, -2, -2 - 2i]) = [1, 2, 3, 4]

Section 9  Factor, Is_prime and Roots  Functions

Factor function calculates factorial of a non-negative integer. For example, factor(3) returns 6.

Factor function has only one parameter. If the parameter is not an integer, it will be truncated to an integer first. If the parameter is negative or cannot be converted to an integer, an error will be reported.

Is_prime function determines whether a real value is a prime or not. For example, is_prime(3.3) returns false while is_prime(97) returns true. Note that this function has only one parameter which must be a real value. If it is not a real value, an error will be reported.

Function roots returns all the roots of a polynomial. Its usage is roots(a, ...). If a is a vector includes N elements (whether real or complex), it returns all the roots (saved in an array) of equation

a[0] * x**(N-1) + a[1] * x**(N-2) + ... + a[N-2] * x + a[N-1] == 0

. If a is single value, then this function needs at least two parameters and returns all the roots (saved in an array) of equation

a * x**(number of parameters - 1) + (first parameter after a) * x**( number of parameters - 2) + … + (second last parameter) * x + (last parameter) == 0

. Note that if the degree of the polynomial is no smaller than 4, Newton Raphson method is used in this function to give out approximation of polynomial roots. This generally takes long time depending on the performance of hardware.

For example, to calculate roots of 3 * x**2 - 4 * x + 1 == 0, user inputs roots([3, -4, 1]) in Command Line and the result is [1, 0.33333333].

To calculate roots of (1+2i) * x**3 + (7-6i) * x**2 + 0.54 * x - 4.31 - 9i == 0, user inputs roots(1+2i, 7-6i, 0.54, -4.31-9i) and gets [0.79288607 + 3.9247084 * i, -0.56361748 - 0.78399569 * i, 0.7707314 + 0.85928729 * i].

Function roots gives the same result as a solve block. However, it doesn’t analyze syntax of statement block so that much faster.

The following example is for the above functions. It can be found in the examples.mfps file in math libs sub-folder in the manual’s sample code folder:

Help

@language:

  test prime, factor and roots functions

@end

@language:simplified_chinese

  测试质数、阶乘和一元多项式求根的相关函数

@end

endh

function PrimeFactRoots()

  print("\nis_prime(3.3) = " + is_prime(3.3))

  print("\nis_prime(97) = " + is_prime(97))

  print("\nis_prime(-97) = " + is_prime(-97))

  print("\nis_prime(1) = " + is_prime(1))

  print("\nis_prime(2) = " + is_prime(2))

  print("\nis_prime(0) = " + is_prime(0))

  print("\nis_prime(8633) = " + is_prime(8633))

  print("\nfact(3) = " + fact(3))

  print("\nfact(63) = " + fact(63))

  print("\nfact(0) = " + fact(0))

  print("\nroots([3, -4, 1]) = " + roots([3, -4, 1]))

  print("\nroots(1+2i, 7-6i, 0.54, -4.31-9i) = " _

    + roots(1+2i, 7-6i, 0.54, -4.31-9i))

Endf

Output of the above example is:

is_prime(3.3) = FALSE

is_prime(97) = TRUE

is_prime(-97) = FALSE

is_prime(1) = FALSE

is_prime(2) = TRUE

is_prime(0) = FALSE

is_prime(8633) = FALSE

fact(3) = 6

fact(63) = 1982608315404440064116146708361898137544773690227268628106279599612729753600000000000000

fact(0) = 1

roots([3, -4, 1]) = [1, 0.3333333333333333333333333333333333333333333333333333333333333333]

roots(1+2i, 7-6i, 0.54, -4.31-9i) = [0.7928860730571022099839052581254713102006395451929364570881977409 + 3.9247083954445877597678511535081536006180195929229657166716945562i, -0.5636174763329694374664831861988500484145796260620965968434731734 - 0.7839956883798520996055087388165005568364007706209239481847346781i, 0.7707314032758672274825779280733787382139400808691601397552754324 + 0.8592872929352643398376575853083469562183811776979582315130401219i]

Summary

MFP programming language provides a complete list of functions for mathematical analysis and scientific calculation. These functions are handy and easy to use.

Among them, functions for expression calculation and calculus accept string based MFP expressions as parameters. Different from graphing functions to be introduced later, these functions are able to recognize predefined variables in an MFP expression. In this case, a predefined variable will be replaced by its value before any calculation.